The modern
development of high-performance computing clusters and the wide distribution of
parallel computing technologies open up a number of new opportunities for
solving problems of mathematical modeling in computational gas dynamics. These
new features include high-grade parametric research and solving optimization
analysis problems. Parametric studies suggest multiple solutions to the direct
problem of mathematical modeling with variations in the defining parameters of the
problem. The defining parameters of the problem include characteristic numbers,
such as the Mach number, Reynolds number, Strouhal number, etc., and the
geometric parameters of the problem. Each of the defining parameters varies in
a certain range of variation with a certain partitioning step. The tasks of
optimization analysis are more complex from a computational point of view. At
each split point of the space of defining parameters, such problems assume the
solution of the inverse problem, which aims to find the extremum of one or
another valuable functional (optimal form, minimal drag coefficient, etc.). Parametric
studies and optimization analysis tasks are the basis of a generalized
computational experiment. A generalized computational experiment allows one to
obtain in discrete form a solution not only for one single task, but for a
whole class of problems. Here the class of problems is determined by the ranges
of change of defining parameters.
However, the
discrete solution itself cannot provide an understanding of the results
obtained. It requires a wide and creative use of the tools of scientific
visualization [1,3] and visual analytics [8–12]. When visualizing the results
of a generalized computational experiment, it is necessary to combine the use
of classical methods of visualization and animation of three-dimensional scalar
and vector fields with visual analytics tools designed for analyzing
multidimensional data. On the one hand, the task becomes much more complicated,
but on the other hand, in the future there is the possibility of obtaining a
solution for a class of problems. Many articles have been devoted to the
development of scientific visualization tools, including [1,3]. Various aspects
of constructing a generalized computational experiment are considered in
sufficient detail in [2, 4–6, 14]. The development of procedures for analyzing
the results of a generalized computational experiment, presented in the form of
a multidimensional data volume, is considered in [7, 13, 15]. This article is
intended to systematize the tasks of visualization arising from the
implementation of a generalized computational experiment, and begin a broad
discussion of such problems and methods for their solution.
A formal description
of a generalized computational experiment is given in sufficient detail in [2,
4–6, 14]. We give below a brief formal description, following [14].According to
[14], a generalized computational experiment involves the splitting of each of
the determining parameters of the problem within a certain range. Thus, a grid
partition is formed for a multidimensional parallelepiped composed of the
determining parameters of the gas dynamics problem under consideration. For
each point of this grid in the space of defining parameters, the problem is
calculated. Formally, this can be written as follows.
Suppose that there is
a reliable numerical method for solving two-dimensional and three-dimensional
non-stationary problems of computational gas dynamics. Then we can for any
point in the space of a countable region and at any time moment obtain a numerical
solution 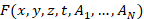 , where
x, y, z are spatial coordinates, t is time,
, where
x, y, z are spatial coordinates, t is time, 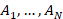 - defining parameters of the problem. As the
defining parameters of the problem, we will keep in mind the characteristic
numbers describing the properties of the flow in question, such as Mach number,
Reynolds number,
Prandtl number,
Strouhal number,
etc., and characteristic geometric parameters. Each of the characteristic
parameters is limited in a certain range:
- defining parameters of the problem. As the
defining parameters of the problem, we will keep in mind the characteristic
numbers describing the properties of the flow in question, such as Mach number,
Reynolds number,
Prandtl number,
Strouhal number,
etc., and characteristic geometric parameters. Each of the characteristic
parameters is limited in a certain range:
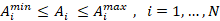
We divide each of the
parameters 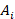 into k-1
parts, so we obtain for each
parameter a partition consisting of k points. The volume of N -
dimensional space formed by the set of defining parameters
into k-1
parts, so we obtain for each
parameter a partition consisting of k points. The volume of N -
dimensional space formed by the set of defining parameters 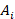 is filled with a set of
is filled with a set of 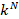 points. Denoting a point from this set as
points. Denoting a point from this set as 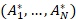 , we arrive at the fact that for each point of
the set it is necessary to obtain a numerical solution of the gas-dynamic
problem
, we arrive at the fact that for each point of
the set it is necessary to obtain a numerical solution of the gas-dynamic
problem 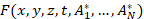 . This
will require solving
. This
will require solving 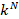 gas-dynamic problems, which is impossible
without the use of parallel computing in multitasking mode. Here we formulated
the classical problem of parametric research. Parametric numerical studies
allow one to obtain a solution not for one specific problem of mathematical
modeling, but for a class of problems specified in a multidimensional space of
defining parameters. Also, such a formal statement allows a numerical study of
optimization analysis problems, when the inverse problem is solved at each
point of the grid partition of the multidimensional space of defining
parameters. Both types of similar problems are considered in the papers [2,
4-6, 14].
gas-dynamic problems, which is impossible
without the use of parallel computing in multitasking mode. Here we formulated
the classical problem of parametric research. Parametric numerical studies
allow one to obtain a solution not for one specific problem of mathematical
modeling, but for a class of problems specified in a multidimensional space of
defining parameters. Also, such a formal statement allows a numerical study of
optimization analysis problems, when the inverse problem is solved at each
point of the grid partition of the multidimensional space of defining
parameters. Both types of similar problems are considered in the papers [2,
4-6, 14].
So, as a result of
a generalized computational experiment, we obtain a numerical solution of the
gas-dynamic problem 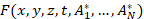 for
each point of space at any time and for each point of partition of the space of
defining parameters
for
each point of space at any time and for each point of partition of the space of
defining parameters 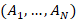 . Let's try to systematize the emerging
tasks of visual presentation of this data. In the course of systematization, we
will proceed from the types of data under consideration.
. Let's try to systematize the emerging
tasks of visual presentation of this data. In the course of systematization, we
will proceed from the types of data under consideration.
A) Here F is
a vector of gas-dynamic functions, such as pressure, density, temperature,
velocity components. For each point of the partitioning of the spatial
countable domain (x, y, z) at the moment of time t we have a
whole set of solutions corresponding to each point of the partition of the
space of defining parameters. From a practical point of view, the usefulness of
such data is small, but such information can be very useful in assessing the
contribution of the determining parameter 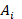 to the total variance at each point of the
computational domain and at any time moment. Here, for visualization at each
point, it is advisable to use a classic spider diagram with normalization to
the range of change of the determining parameter.
to the total variance at each point of the
computational domain and at any time moment. Here, for visualization at each
point, it is advisable to use a classic spider diagram with normalization to
the range of change of the determining parameter.
B) For each split
point of the space of defining parameters 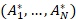 we have a calculated flow pattern in the
selected region of space (the calculated region). This makes it possible to
apply the entire rich set of scientific visualization methods and software [1,
3], developed earlier for gas dynamics problems. Possible types of informative
visual representations include:
we have a calculated flow pattern in the
selected region of space (the calculated region). This makes it possible to
apply the entire rich set of scientific visualization methods and software [1,
3], developed earlier for gas dynamics problems. Possible types of informative
visual representations include:
- visualization
of scalar and vector fields in parallel sections of the computational domain
and cross-sections;
- animation of
scalar and vector fields in the constructed sections;
- construction of combined visual representations.
Figure 1 shows an
example of a visual presentation using cross-sections of the process of
propagation of a low-velocity air jet in the computational domain [1]. Figure 2
shows an example of a combined presentation - a combination of temperature
distribution in parallel sections with surfaces “stretched” on the velocity
vectors [1].
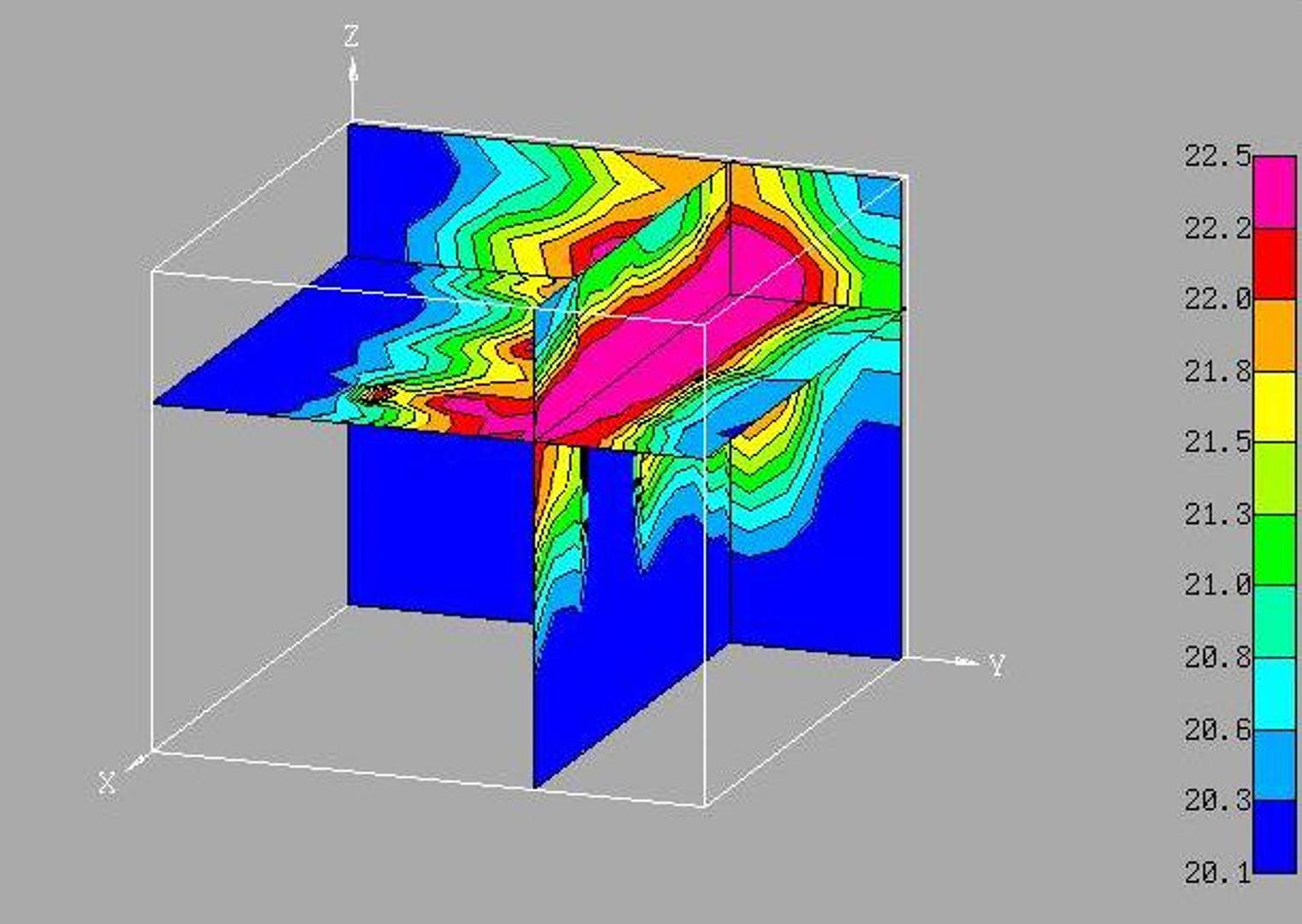
Fig. 1. An example of the use of
cross-sections [1].
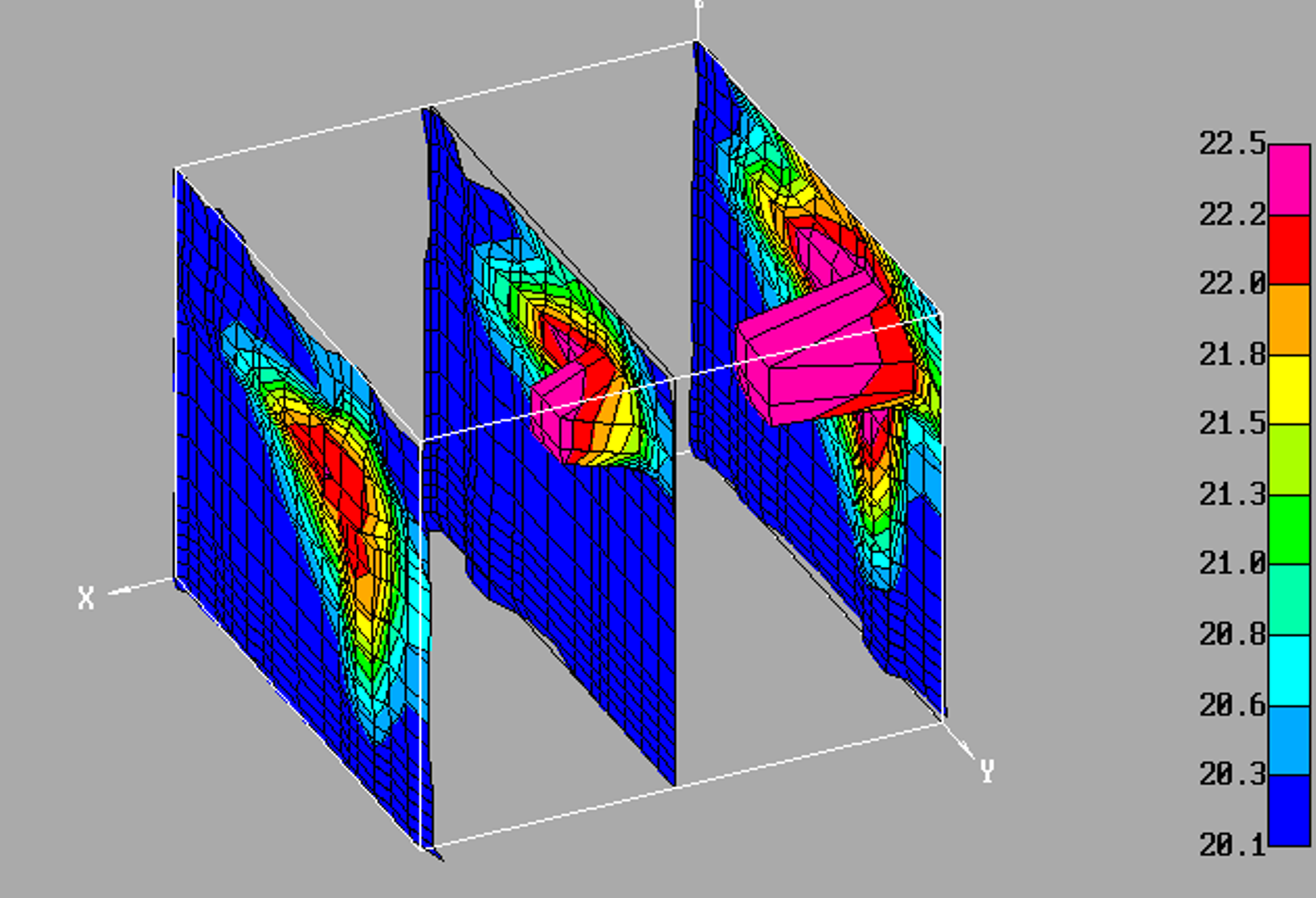
Fig. 2. Combined representation - a combination of temperature distribution in
parallel sections with surfaces “stretched” on the velocity vectors [1].
We can create
similar representations in the most diverse combinations for each fixed point
of a partition of the space of defining parameters 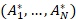 .
.
Here we have a new
opportunity to construct the boundaries of change of the defining parameters of
interest from 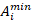 to
to 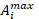 for each
for each 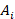 . This can be useful, for example, in the
visualization of separation zones, where it is possible to single out the
limits of the change in the position of the separation zones, depending on the
choice of the determining parameter. It should be noted that such visual presentations
for a particular class of problems can be created on the basis of already
existing methods and algorithms implemented in many software systems, such as
ParaView, VizIt, TecPlot.
. This can be useful, for example, in the
visualization of separation zones, where it is possible to single out the
limits of the change in the position of the separation zones, depending on the
choice of the determining parameter. It should be noted that such visual presentations
for a particular class of problems can be created on the basis of already
existing methods and algorithms implemented in many software systems, such as
ParaView, VizIt, TecPlot.
C) From a
practical point of view, when solving problems of computational gas dynamics,
the primary interest to the user, as a rule, are valuable functionals
calculated using the already computed gas-dynamic functions in the
computational domain. The role of such a functional can be played by the total drag
coefficient of a body in the flow or the friction drag coefficient for viscous
problems. When analyzing the conditions for the emergence and decay of
space-time structures in a flow field, such a functional can be the
characteristic time of the structure's existence.
Here we come to
the classical tasks of visual analytics [8-12], where the goal is to obtain
maximum information about the multidimensional data array 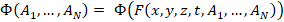 and
hidden relationships between its defining parameters. For these purposes, a
sufficient number of approaches have been developed [8-10]. One of the possible
approaches presented in [6,13-15] is dimension reducing of the studied space of
defining parameters to three, the visual representation of dependence obtained
for
and
hidden relationships between its defining parameters. For these purposes, a
sufficient number of approaches have been developed [8-10]. One of the possible
approaches presented in [6,13-15] is dimension reducing of the studied space of
defining parameters to three, the visual representation of dependence obtained
for 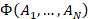 and approximation of this dependence using
a set of geometric primitives. The purpose of this approach is to represent the
dependence of
and approximation of this dependence using
a set of geometric primitives. The purpose of this approach is to represent the
dependence of 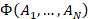 in an analytical form. If successful, this
makes it possible to construct the obtained results of mathematical modeling in
the form of a physical law for the class of problems in question. This area of
research involves the development of a large number of approaches and software tools.
in an analytical form. If successful, this
makes it possible to construct the obtained results of mathematical modeling in
the form of a physical law for the class of problems in question. This area of
research involves the development of a large number of approaches and software tools.
Modern development
of computing systems and technologies allows to organize the construction of a
generalized computational experiment in modeling problems of computational gas
dynamics. The construction of such an experiment is based on numerical
parametric studies and the solution of optimization analysis problems. Solving
such problems implies a multiple solution to the direct problem of numerical
modeling of a gas-dynamic process with various input data. The defining
parameters of a class of problems, such as the characteristic Mach number,
Reynolds number, geometric parameters, etc., vary in certain ranges with a
certain partitioning step. As a result, the resulting solution is a
multidimensional amount of data. To analyze this volume, visualization is
necessary. The paper attempts to systematize and briefly describe some types of
problems arising from processing the results of a generalized computational
experiment. The aim of the work is to begin a broad discussion of the tasks of
visualization in a generalized computational experiment and methods for their
solution.
[1]
Bondarev A. E. and Bondarev E. N. Visualization Functions in Computational
Fluid Dynamics / Obshcheros. NauchnoTekhn. Zh. Polet (Mashinostr, Moscow, 2000),
No. 10, pp. 53–60 [in Russian].
[2]
Bondarev A. E. Optimization of hybrid difference scheme taking into account the
influence of viscosity and turbulence based on the solution of inverse problems
// Conference proceedings « High performance computing in problems of
mechanics and physics», Moscow, 2009. p. 39-44.
[3] Bondarev A.E., Galaktionov V.A.,
Chechetkin V. M. Analysis of the Development Concepts and Methods of Visual
Data Representation in Computational Physics / Computational Mathematics and
Mathematical Physics, 2011, Vol. 51, No. 4, pp. 624–636.
[4] Bondarev A.E. Analysis of unsteady space-time structures
using the optimization problem solution and visualization methods // Conference
proceedings of 22-th International Conference on Computer Graphics and Vision,
Lomonosov Moscow State University, October 01-05, 2012, p.184-188.
[5]
Bondarev A.E., Galaktionov V.A. Analysis of Space-Time Structures Appearance
for Non-Stationary CFD Problems / Proceedings of 15-th International Conference
On Computational Science ICCS 2015 Rejkjavik, Iceland, June 01-03 2015,
Procedia Computer Science. Vol. 51. P. 1801–1810.
[6]
Bondarev A.E., Galaktionov V.A. Multidimensional data analysis and
visualization for time-dependent CFD problems / Programming and Computer
Software. 2015. Vol. 41. ¹. 5. P. 247–252. DOI: 10.1134/S0361768815050023
[7] Bondarev
A.E., Galaktionov V.A., Shapiro L.Z. Processing and visual analysis of
multidimensional data / Scientific Visualization. V.9, ¹ 5, ñ.86-104, 2017, DOI:
http://doi.org/10.26583/sv.9.5.08
[8] Thomas
J. and Cook K. Illuminating the Path: Research and Development Agenda for
Visual Analytics. IEEE-Press, 2005.
[9] Kielman,
J. and Thomas, J. (Guest Eds.) (2009). Special Issue: Foundations and Frontiers
of Visual Analytics / Information Visualization, Volume 8, Number 4, p. 239-314.
[10] Keim
D., Kohlhammer J., Ellis G. and Mansmann F. (Eds.) Mastering the Information
Age – Solving Problems with Visual Analytics, Eurographics Association, 2010.
[11]
Gorban A., Kegl B., Wunsch D., Zinovyev A. (Eds.), Principal Manifolds for
Data Visualisation and Dimension Reduction, LNCSE 58, Springer, Berlin –
Heidelberg – New York, 2007.
[12]
Gorban A.N., Zinovyev A. Principal manifolds and graphs in practice: from
molecular biology to dynamical systems / International Journal of Neural Systems.
2010. Vol. 20. ¹. 3. P. 219–232. DOI: 10.1142/S0129065710002383
[13]
Bondarev A.E., Galaktionov V.A. and Shapiro L.Z. Processing and visual
analysis of multidimensional data / Scientific Visualization, 9(5) 2017, p
86-104.
[14]
Bondarev A.E. On the Construction of the Generalized Numerical Experiment in
Fluid Dynamics // Mathematica Montisnigri, Vol. XLII, 2018, p. 52-64.
[15] A.E.
Bondarev, A.V. Bondarenko, V.A. Galaktionov (2018) Visual analysis procedures
for multidimensional data. Scientific Visualization 10.4: 109 - 122, DOI:
10.26583/sv.10.4.09


